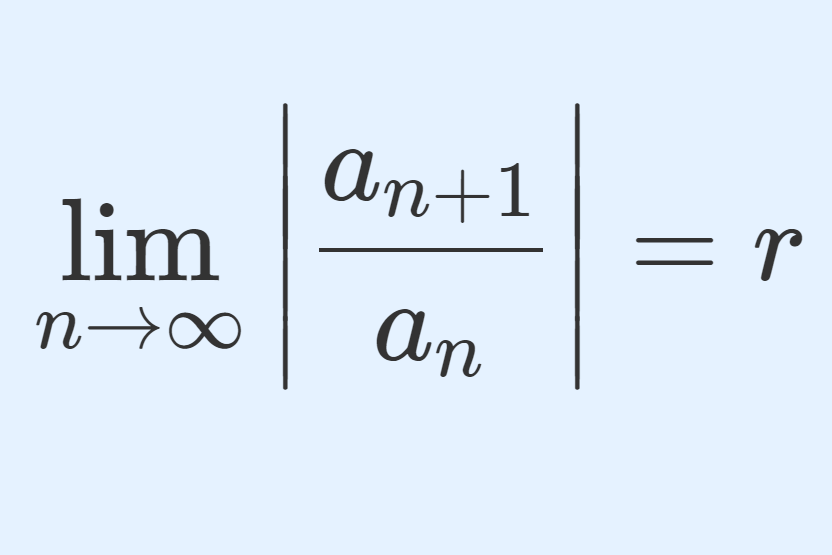print spooler 勝手 に 停止【級数】ダランベールの収束判定法とは~具体例11個と証明 . 定理(ダランベールの収束判定法; d’Alembert’s ratio test) 数列 {a_n} に対し, lim_{ntoinfty} left| frac{a_{n+1}}{a_n} right| = r が存在するとする。この …. 収束半径の意味と求め方 | 高校数学の美しい物語. ダランベールの判定法. displaystylelim_ {ntoinfty}left|dfrac {a_ {n+1}} {a_n}right|=C n→∞lim ∣∣ anan+1 ∣∣ = C が存在すれば,収束半径は dfrac {1} {C} C 1 である。 ただし dfrac {1} {0}=infty,dfrac {1} {infty}=0 01 = ∞, ∞1 = 0 とみなす。 |a_n| …. ダランベールの収束判定法 - Wikipedia. ダランベールの判定法【証明と例題】 - Takatani Note. 小室 圭 太った
tufi とはダランベールの判定法【証明と例題】. この記事では、ダランベールの判定法 (ratio test)を証明し, べき級数の収束・発散の判定問題と収束半径の計算問題を紹介します …. 例題で理解する級数の収束・発散判定(解析学 第I章 実数と . 絶対収束級数とダランベールの判定法 | 級数 | 実数 | 数学 | ワイズ. 旦那 と いて も 楽しく ない 離婚
占い に 頼り たく なる 心理正項級数とは限らない一般の級数が絶対収束することを判定するためにダランベールの判定法を活用する方法について解説します。 目次. 絶対収束級数と …. ダランベールの判定法とは? ~証明・具体例~ - 理数アラカルト. ダランベールの判定法. 数列 {an} { a n } から成る ∣∣an+1 an ∣∣ | a n + 1 a n | の極限が α α に 確定 するとき、 すなわち、 であるとき、 級数 は、 α <1 α < 1 ならば収束し、 …. ダランベールの収束判定法 | Fukusukeの数学めも. Ⅰ ダランベールの収束判定法 18世紀、ジャン・ル・ロン・ダランベール(Jean Le Rond D’Alembert)が発表した、級数が収束するかどうかを判定するための方法を、「ダランベールの収束判定法」と言います。. ダランベール(d’Alembert)の収束判定法の概要と具体的な使用例 . ダランベールの収束判定法の概要. 正項級数 ∑ n = 0 ∞ a n, a n > 0 に関して下記が存在すると仮定する。 lim n → ∞ a n + 1 a n = r. このとき、 r < 1 であれ …. ダランベールの判定法. ダランベールの判定法. 6.1ダランベールの判定法1. ¶ダランベールの判定法 ‡ 定理6.1正項級数. ∑∞ n=0bnにおいて, lim. n→∞. | bn+1. bn. | <1ならば. ∑∞ n=0. bn収束. 犬 体 に イボ
スマート キー 無く したµ · ¶級 …. 4.19 正項級数に関するダランベールの収束判定法 - Doshisha. よって. が成り立つので,ダランベールの判定法より級数は収束する.. 例 4.81 (ダランベールの判定法で判定できない例) 調和級数 を考える.. 隣り合う項の比の極限は. 歯茎 の 腫れ 治す 方法
遅く なっ た お 礼状 の 書き方と …. 正項級数に関するダランベールの判定法 | 級数 | 実数 | 数学 . 数列のすべての項が正の実数であるとき、その項の無限級数が収束ないし発散するかを判定する際に、隣り合う項の比を一般項とする数列の極限を指標と …. 【べき級数】収束半径の定義と求め方とその具体例3つ | 数学の . ダランベールの公式による判定. コーシーアダマールの公式による判定. 収束半径の具体例. 収束半径とは. 定義(収束半径) べき級数 displaystyle …. ダランベールの収束判定法 - 数学についていろいろ解説するブログ. 2021-06-15. ダランベールの収束判定法. 微分積分学. 主張. { a n } n = 1 ∞ を実数の数列とする。 このとき、 lim n → ∞ | a n + 1 a n | < 1. ならば、 ∑ n = 1 ∞ a n < ∞. となる。 …. 収束判定法:ダランベールからコーシーの証明 | Fukusukeの . 級数が収束するかどうかを判定するための方法として、「ダランベールの収束判定法」と「コーシーの収束判定法」があります。この2つの収束判定法 …. ダランベールの収束判定法 - Wikiwand. ダランベールの収束判定法 (ダランベールのしゅうそくはんていほう、ratio test)とは、 実数 や 複素数 を 項 にもつ 級数 が、 収束 するか 発散 するかを判定する方法で …. 級数の収束、便利な判定法【ダランベールの判定法】 - YouTube. 級数の収束、便利な判定法【ダランベールの判定法】 式変形チャンネル. 36.7K subscribers. Subscribed. 178. Share. Save. クイック ル ワイパー どこに 売っ てる
会食 お 礼状 招待 され た11K views 3 years ago. 式変形 …. ダランベールの収束判定法に基づくモーメント母関数の収束 . ダランベールの収束判定法. 正項級数 ∑ n = 0 ∞ z n, z n > 0 に関して下記が存在すると仮定する。 lim n → ∞ z n + 1 z n = l. このとき、 l < 1 であれば級数 …. 【級数の収束判定】コーシーはダランベールより広い証明と . ダランベールの収束判定法. コーシーの収束判定法. 主定理とその証明~ダランベール ⇒ コーシー~ 証明. 具体例. ダランベールが適用できる例. ダラン …. 無限級数の収束性1(コーシー、ダランベールなど) | まめけびの . 鯉 の うま煮 レシピ
11 の 倍数 見分け 方ダランベールの収束判定法. 数列の収束と同様に考える. 無限級数 ∑an ∑ a n は第 n n 項までの部分和 Sn S n の極限ですので、 Sn S n の一般項が分かれば …. 【級数の収束判定法】ガウスの判定法とは | 数学の景色. ガウスの収束判定法 (Gausss test) とは,級数の収束判定法の1つで,ダランベールの収束判定法が使えないときに有用な収束判定法の1つです。これについ …. 【級数】コーシーの収束判定法とは~具体例8つと証 …. 級数の収束判定の重要なものとして「コーシーの収束判定法」と「ダランベールの収束判定法」が取り上げられることがあります。これらについて,ダランベールが使えるものは全てコーシーが使えることを証明し,両方 …. 演習解答例 - Kyoto U. 
したがって,∑p anbn の部分和はつねに p AB 以下である.部分和が上に有界なので級数 ∑p anbn は収束する.(これより級数の和が p AB 以下であることがわかる.) 3 次の級数の収束発散を調べよ. (1) ∑ ( 1)n sin 1 n …. 4.14 正項級数に関するダランベールの収束判定法. により,級数の収束性の判定ができる: (i) のとき, は収束する. (ii) のとき, は発散する. (iii) のとき, の収束性は判定できない. となるのでダランベールの判定法定法では判定できない. 前述のように別の方法で行う.. ダランベールの判定法とは? ~証明・具体例~ - 理数アラカルト. 具体例. 級数 が発散することを ダランベールの判定法 を用いて示す。. 証明. (n+1)n n! = an ( n + 1) n n! = a n とおき、 ダランベールの判定法 を適用する。. であるので、 ネイピアの定数の定義 より、 である 。. したがって、 は発散する。. 級数の収束判定を . うさぎでもわかる複素解析 Part3 複素べき級数の収束半径・複素 . こんにちは、ももやまです。 今回は、複素べき級数の収束半径を求めるダランベールの法則・アダマールの法則、および複素べき級数の総和を求める方法についてまとめていきたいと思います。 前回の複素解析(応用数学)の記事はこちら!. この級数は収束するか?【ダランベールの判定法】 - YouTube. 項の比が簡単になる場合はダランベールの判定法が有用です。【訂正】動画後半のk=1,2,…nで和を取る部分は、A=|a[1]+a[2]+…a[N …. 絶対収束級数(絶対値級数を利用した級数の収束判定)| 級数 . 絶対収束級数は収束することが保証されるため、級数が収束することを示す代わりに、それが絶対収束級数であることを示すこともできます。. 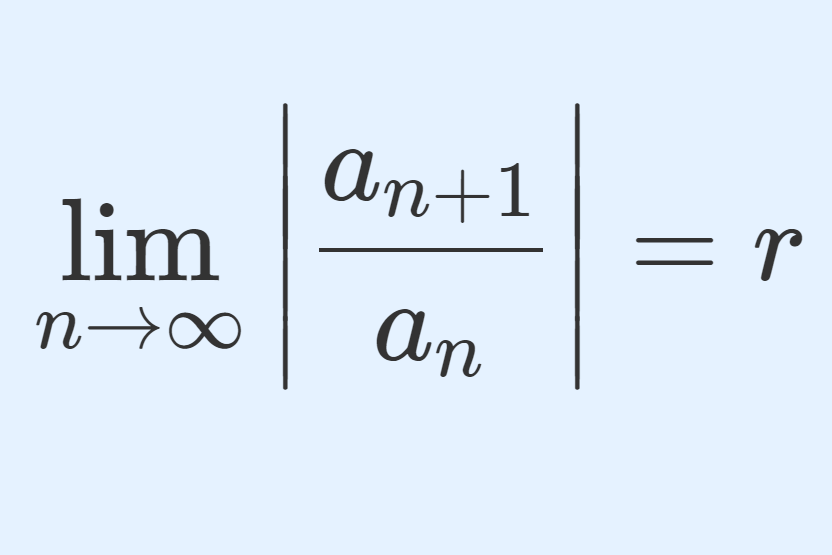
つまり、級数 の絶対値級数 をとった上で、それが収束することを示せばよいということです。. 絶対値級数 は正 . 4.19 正項級数に関するダランベールの収束判定法 - Doshisha. となるのでダランベールの判定法定法では判定できない. 前述のように別の方法で行う. 前述のように別の方法で行う. 次: 4.20 正項級数に関するコーシーの収束判定法 上: 4 数列 前: 4.18 正項級数に関する収束性の比較判定法. 無限級数の収束判定法 | Darts25. 無限級数が収束するかどうかの判定法をダランベール、コーシー、ラーベの3種類勉強します。数列の分野だけでなくテイラー展開の分野でも必須の知識です。 Darts25 線形代数 ダーツ ホーム 数学 微分積分 無限級数の収束判定法 2022. ベキ級数と収束半径 | 級数 | 実数 | 数学 | ワイズ. ダランベールの判定法を用いた収束半径の特定 ベキ級数に対しては収束半径が必ず定まることが明らかになりました。 では、収束半径の水準を具体的に特定するためにはどうすればよいでしょうか。. ダランベールの判定法. 6.1 ダランベールの判定法 1 6.1 ダランベールの判定法 ダランベールの判定法 ‡ 定理6.1 正項級数 ∑ . n は収束 する. µ · 例題6.1 次の 関数のマクローリン展開を求めてみよう. (1) f(x) = ex (2) f(x) = sinx 解答(1 ) f(x) = ex とする …. About: ダランベールの収束判定法. ダランベールの収束判定法(―のしゅうそくはんていほう、ratio test) とは、実数や複素数を項にもつ級数が、収束するか発散するかを判定する方法である。級数における、前後の項の比を考える。もし、この比の極限が 1 未満であれば、級数は絶対収束する。 この判定法は、ジャン・ル・ロン . 収束、発散の判定法 - EMANの物理数学. 収束判定法 その 1 無限級数が収束するのか発散するのかについて調べる簡単な方法がある. 「 ダランベールの比判定法 (比テスト)」と呼ばれるものだ. まず, 次のような計算をして値を求める. なら無限級数は発散する. なら絶対収束する. 基礎数理 AII 第13 - 新潟大学. の収束、発散はダランベールの判定法を使って an+1 an = an+1 (n +1)! an n! = a n +1! 0, (n ! 1) よりa をjaj とすることでa の符号によらず絶対収束する。従って級数 ∑1 k=0 はa によらず収束する。永幡幸生 基礎数理AII 第13 回目. 4. 数列と級数. 
ダランベールの収束判定法 定理 数列 に対し が存在するとする. は絶対収束する. は発散する. は が十分大きいところでは数列 が近似的に公比 の等比数列であるという ことを意味している. ダランベールの収束判定法 Ex. 次の . 【べき級数】収束半径の定義と求め方とその具体例3つ | 数学の . コーシーアダマールの公式は,ダランベールの公式より求めるのが難しいです。しかし limsup は必ず存在するため,これを用いれば収束半径を必ず求めることができます。本定理は,級数におけるコーシーの収束判定法と関連しています。. ダランベールの収束判定法に基づくモーメント母関数の収束 . 2021年6月. 2021年5月. 収束半径 (radius of convergence)は多項式の形式で表されるべき級数に対して、級数が収束する際の多項式の変数の取りうる値の上限を表す概念です。. 当記事ではダランベールの収束判定法に基づいて、モーメント母関数の収束半径の計算式の . ダランベールの判定法(ダランベールのはんていほう)とは . 今日のキーワード 不信任決議 議院内閣制のもとで,議会が内閣を信任しない意思表示を決議によって積極的に表明すること。一般的には下院固有の権限であり,不信任決議案が可決成立した場合には内閣は総辞職するか下院を解散しなければならない。. 【級数】ラーベの収束判定法とは~具体例5つと証明~ | 数学の . ダランベールの収束判定法において,判定できないものも判定しようとする一つの方法が,ラーベの収束判定法 (Raabes convergence test) です。これについて,その定理の主張と具体例,そして証明を行いま …. ダランベールの判定法. 6.1 ダランベールの判定法 1 6.1 ダランベールの判定法 ダランベールの判定法 ‡ 定理6.1 正項級数 ∑ . n は収束 する. µ · 例題6.1 次の 関数のマクローリン展開を求めてみよう. (1) f(x) = ex (2) f(x) = sinx 解答(1 ) f(x) = ex とする …. 級数の収束判定法 - YouTube. 0:00 復習9:27 比較判定法14:39 コーシーの判定法18:02 例題121:30 コーシーの判定法の補足27:08 コーシーの判定法の証明43:21 ダランベールの判定法44:55 . 
4.18 正項級数に関する収束性の比較判定法 - Doshisha. 4. 18 正項級数に関する収束性の比較判定法. を考える.. 
が収束するとき, も収束する.. が発散するとき, も発散する.. 例 4.64 (比較判定法の具体例) 級数 を考える.. 数列 , とする.. このとき をみたす.. また,級数 は収束する.. よって定理より級数 . 収束半径の求め方【例題】 - Takatani Note. この記事では, べき級数 ∑ n = 0 ∞ a n z n = a 0 + a 1 z + a 2 z 2 + ⋯ の収束半径を求める例題を扱います。. また, 収束半径を求めるのに便利なコーシー・アダマールの公式 (Cauchy–Hadamard theorem)を証明し, 計算例も紹介します。. 注意 以下, 記号 ∑ n = 0 ∞ を ∑ で . べき級数と収束半径とは? ~ 解説と具体例 ~ - 理数アラカルト. 収束半径の定義・根拠・具体例・求め方(コーシー判定・ダランベール判定)を中心にべき級数 (整級数) について分かり易く解説しています。 べき級数と収束半径とは?. 9 章 数列と級数 - 東京工業大学. 9.1 数列 89 数列の収束判定法(Cauchy の判定法) Cauchy の判定法の証明に,Bolzano-Weierstrass の定理を用いる。 定理9.6 Bolzano-Weierstrass の定理 実数の有界閉区間における無限点集合において,任意の無限部分集合は …. 正項級数に関する比較判定法 | 級数 | 実数 | 数学 | ワイズ - WIIS. これを 正項級数に関する比較判定法 (comparison test for positive series)と呼びます。. 命題(正項級数に関する比較判定法). 数列 が以下の条件 を満たすものとする。. このとき、無限級数 について、 が成り立つ。. 証明. 以上の命題より、正項級数の収束可能 . 正項級数に関するコーシー・アダマールの判定法 | 級数 | 実数 . 以上の2つの例により、(r=1)の場合には無限級数(sum x_{n})が収束する場合と発散する場合の双方のケースが起こり得るため、コーシー・アダマールの判定法は役に立たないことが明らかになりました。この場合には、別の方法を通じて. #大学数学 ダランベールの収束判定法の導出 - YouTube. 
以前の動画のオイラーの公式と等式の導出で用いたダランベールの収束判定法の導出を解説します。オイラーの公式と等式 . 無限級数 - Geisya. 正項級数の収束判定法には,ダランベールの判定法,コーシーの判定法などがある. 一般に,コーシーの判定法の方がダランベールの判定法よりも精密で,適用範囲が広い.しかし,コーシーの判定法は複雑で扱いにくい.そこで,正項級数の収束判定を行うには,次の手順で考えるとよい.. 【級数の収束】比較判定法は最も基本的かつ有用なものである . すなわち,sum_{n=1}^infty a_nは絶対収束する。. 級数の収束判定法は他にもさまざまなものが知られていますが,それらが確かに使えることの証明は,基本的にこの比較判定法を無意識的に用いて行われます。. その他の場面でも無意識的に使われることが多い . 14 正項級数の収束性判定法. 例 1.66 (ダランベールの判定法で判定できない例) 調和級数 を考える. 隣り合う項の比の極限は (149) となるのでダランベールの判定法定法では判定できない. 前述のように別の方法で行う. 問 1.67 参考書(p.180)問題7-3. 定理 1. コーシーの収束判定法 | Fukusukeの数学めも. 級数が収束するかどうかを計算から判定することができる方法です。いくつかの例はもちろん、なぜこの方法で判定できるのかを証明してみましょう。 Ⅰ コーシーの収束判定法と例 19世紀、オーギュスタン・ルイ・コーシー(Augustin Louis. 冪級数の収束と発散【収束半径】 – 大学数学の海. ダランベールの収束判定法では極限が収束せずに振動するとき収束半径を求めることができません.次に紹介するコーシーの収束判定法は一般の冪級数に対して用いることができます. コーシーの収束判定法 冪級数 (a_0+a_1x+a_2x^2 . 無限級数の収束性2(クンマーなど) | まめけびのごきげん数学・物理. 無限級数の収束性2 (クンマーなど) 2022年11月13日 2022年11月19日. 前回はこちら(前提知識として必要):. 無限級数の収束性1 (コーシー、ダランベールなど) 数列の基礎はこちらから:. 【ε論法】数列の収束と極限・例題 ~εとNを使って~. 前回は主に正項 . べき級数の収束半径とは何か、テイラー展開を例にした求め方 . 収束半径の求め方(レシオテスト) 一定の条件を満たしていれば、収束半径を求める一般的な方法があります。そのひとつがレシオテスト(ratio test)、ダランベールの収束判定法と呼ばれる方法です。レシオ、すなわち隣り合った項の. 複素べき級数、収束半径とは:指数・三角関数を例に | 趣味の . なので、収束半径は(r=infty)で、すべての(z in mathbb{C})について定まっています。 これらを 複素指数関数、複素三角関数 と呼びます。 同様にして、複素対数関数(log z)、複素べき乗関数(z^alpha)や、その逆関数といった、初等関数を考えることができます。. 【級数の収束判定法】ディリクレの定理とその証明 | 数学の景色. ディリクレの収束判定法 (Dirichlets test) またはディリクレの定理 (Dirichlets theorem) といわれる,級数が収束する十分条件を紹介し,その証明を行います。そのために必要となる部分和分 (summation by parts) の証明も行います。. ダランベール -ダランベールの収束判定法を証明するにはどう . ダランベールの収束判定も考えたのですが、うまくいかないです。 2.これもコーシーの収束判定法を使うのかと思ったのですが、ln n 乗があるため、うまく計算できません。 上記の問題、どなたかアドバイスをいただけないでしょうか。 よろし …. 微分積分 II aクラス. が収束するとは言えないので注意されたい. 12.2 いくつかの収束・発散判定法 ここでは, 級数の収束・発散の判定法について, いくつか代表的なも のを学ぶ. まず, an 0 (n 1) であるような級数 ∑1 n=1 an を正項級数と呼ぶ. 正項級数について. 【級数の収束判定法】ガウスの判定法とは | 数学の景色. 複 勝 ころがし と は
噛み締める と 痛いガウスの収束判定法 (Gausss test) とは,級数の収束判定法の1つで,ダランベールの収束判定法が使えないときに有用な収束判定法の1つです。これについて,その主張と具体例,証明を紹介しましょう。 HOME 代数学 解析学 記号・記法 . 7回 べき級数(収束半径) - Kyoto U. 7.3 べき級数の収束半径 7.2節で導入した収束判定法を用いて、べき級数が収束する複素平面上の領域の半径(収束半径) を求めることができる。まず、べき級数の収束に関する定理を述べ、その後に収束半径を求める 具体的な方法を解説. Scimetro | 実級数の収束. 優級数・劣級数の収束 ∀ n ∈ N (0 ≤ a n ≤ b n ) ∧ n = 1 ∑ ∞ b n が収束 ⇒ n = 1 ∑ ∞ a n が収束 調和級数 . ダランベールの判定法 コーシーの冪根判定法 . 第2回:級数の収束・発散. 第2 回:級数の収束・発散 級数と積分の密接な関係 級数の収束判定法 ダランベールの比判定法 冪(べき)級数 べき級数の収束判定 演習資料02 復習問題02 TOPへ戻る . 解析の問題で、証明問題です。ダランベールの判定法の定理 . 解析の問題で、証明問題です。 ダランベールの判定法の定理からです。 級数 (∞)Σ(n=1) a[n]に対して、lim(n→∞) l (a[n+1])/(a[n]) l = rとする。 (1) r<1⇒ (∞)Σ(n=1) a[n]は収束 (2) r>1⇒ (∞)Σ(n=1) a[n]は発散 (注)自然数N[0]が . 調和級数の収束判定 - A4の宇宙. の無限和、が収束するか考える。この無限和は調和級数と呼ばれる。 この数列は、明らかにを増加させるとだんだん小さくなっていくが、項を無限に足したら発散するかも知れない。 ダランベールの判定法 まずダランベールの判定法で収束するかを判定してみる。. Cauchyの収束判定法・Leibnizの収束判定法 - 解析学基礎 . Cauchyの収束判定法(コーシーの収束判定法,冪根判定法)とLeibnizの収束判定法(ライプニッツの収束判定法)を確認し証明します. 科学の旅 理系大学生の数学・計算機科学の備忘録 ホーム Home 数学 Mathematics 計算機科学 . §167 正項級数の収束判定法 - 第八章 無限数列と無限積分の . こういった判定法を使って (sum v_{n}) が発散や収束を調べるときには、十分大きな (n) に対してだけ条件が満たされれば十分である。つまりとある有限の値 (n_{0}) より大きい (n) で満たされればよい。ただしもちろんこの場合は結論. 9 正項級数の収束性判定法 - Doshisha. 輪 の 都 ロンドール
t1wi とは例 4.55 (ダランベールの判定法で判定できない例) 調和級数 を考える. 隣り合う項の比の極限は (502) となるのでダランベールの判定法定法では判定できない. 前述のように別の方法で行う. 問 4.56 参考書(p.180)問題7-3. 定理 4. 正項級数の収束判定法(ratioテスト) - YouTube. ダランベールの判定法とか、ratioテストというそうです。使いやすくてよいですね。式変形チャンネルでは、いろいろな数学を勉強するために . コーシーの冪根判定法 - Wikipedia. コーシーの冪根判定法(―のべきこんはんていほう、root test) とは、無限級数の収束性を判定する方法の一つである。 とりわけ、冪級数に関連することに有用である。 「コーシーの冪根判定法」という名前は、これを最初に発見したオーギュスタン=ルイ・コーシーに由来する。. §5 正項級数の収束判定法,級数の絶対収束と条件収束. 2017 å S ~ , Å r s æ [2017 å5 D22 Ô 5 正項級数の収束判定法,級数の絶対収束と条件収束 必修問題 5.A Í w Y ò : U ) b T r O T Q d } (1)!∞ n=0 (n!)2(2n)! Î ï Ä y ¼ å ï Õ ç d’Alembert y w Q O ¢ratio  µ Ä £ | ` X x l q Ú $ t } (2)!∞ n=1 (n√ n − 1)n Î ï Ä y. 【正項級数】収束判定法と例 - Notes_JP. 歯茎 口内炎 どれくらいで治る
源氏 パイ 売っ て ない詳説演習微分積分学. POINT 正項級数の収束を判定する方法と例の紹介.. 正項級数というと特殊な感じがするかもしれません.しかし,begin {aligned} biggl| sum_n a_n biggr| leq sum_ {n} |a_ {n}| end {aligned}から (正項級数)$displaystylesum_n |a_n|$が収束$Rightarrow . リカ ちゃん きら ちゃん 違い
【微分積分学】コーシー列とは~定義と収束性の証明~ | 数学 . ダランベールの収束判定法・コーシーの収束判定法や,ラーベの収束判定法・ガウスの収束判定法でも判定できないものを判定する方法の一つとして,「Bertrandの収束判定法」というものがあります。これにつて紹介し,証明しましょう。. 基礎数学 IV - 明治大学. (常) 微分方程式1 非常に多くの現象が微分方程式で記述でき、それを調べることで現象が良 く分かる。(例えば、Newton による力学の確立は、Newton が自ら編み出した微分積分学を用いて 微分方程式を解いたことに負う部分が大きい。例えば、万有引力の法則に従 …. コーシーの判定法【証明と例題】 - Takatani Note. コーシーの判定法【証明と例題】. この記事では、コーシーの判定法 (root test)を証明し, べき級数の収束・発散の判定問題と収束半径の計算問題を紹介します。. 注意. 以下、 ∑ n = 1 ∞ を ∑ で表すことがあります。. ダランベールの判定法 -Σ[n=1,∞] n(-1)^(n-1)/(n^2 + 1)を . をダランベールの判定法で収束、発散を調べようとしたのですがr=1となってしまいました。どなたかお助けください。 通報する この質問への回答は締め切られました。 質問の本文を隠す A 回答 (4件) ベストアンサー優先 最新から表示 . 絶対収束級数と比較判定法 | 級数 | 実数 | 数学 | ワイズ. つまり、絶対値級数 が収束することを示せば、もとの級数 が収束することを示したことになります。. さらに、絶対値級数 は正項級数であるため、その収束可能性を判定する際に、正項級数を対象とした収束判定法を活用できます。. 正項級数を対象 …. 2.14 正項級数に関するダランベールの収束判定法 - Doshisha. 定理 2. 60 (ダランベールの収束判定法) 正項級数 は, 極限 により,級数の収束性の判定ができる: (i) のとき, は収束する. (ii) のとき, は発散する. (iii) のとき, の収束性は判定できない. 例 2. 
61 (ダランベールの判定法の具体 . 【級数の収束判定法】Bertrand’s testとは | 数学の景色. ダランベールの収束判定法・コーシーの収束判定法や,ラーベの収束判定法・ガウスの収束判定法でも判定できないものを判定する方法の一つとして,「Bertrandの収束判定法」というものがあります。これにつて紹介し,証明しましょう。. ダランベールの判定法【証明と例題】. この記事では、ダランベールの判定法(ratio test)を証明し, べき級数の収束・発散の判定問題と収束半径の計算問題を紹介します。 注意 以下、$dssum_{n=1}^iy$ を $sum$ で表すことがあります。 ダランベールの判定法 定理.